今月の額面広告に掲載されている問題はこれだ!
学習院中等科
2016年06月掲載
2016年 学習院中等科入試問題より
- 問題文のテキストを表示する
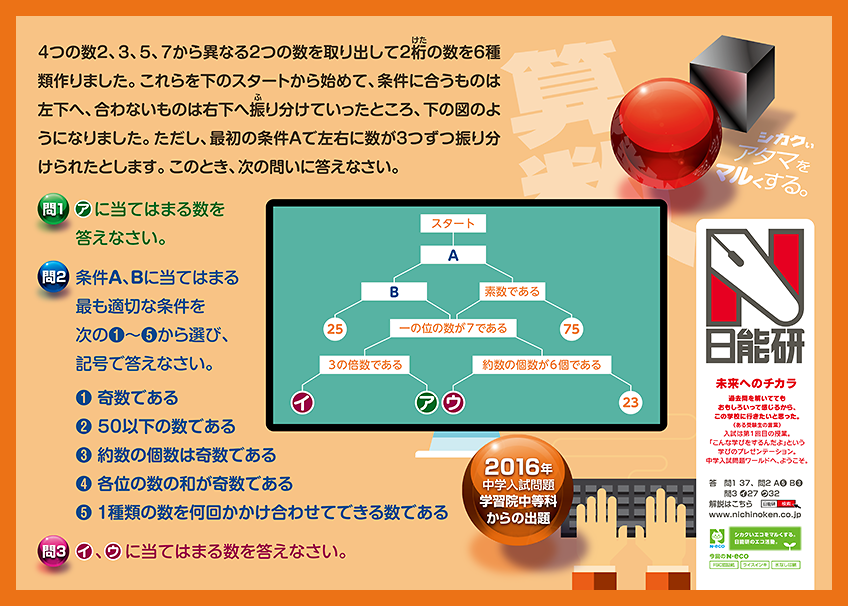
4つの数2、3、5、7から異なる2つの数を取り出して2桁(けた)の数を6種類作りました。これらを下のスタートから始めて、条件に合うものは左下へ、合わないものは右下へ振(ふ)り分けていったところ、下の図のようになりました。ただし、最初の条件Aで左右に数が3つずつ振り分けられたとします。このとき、次の問いに答えなさい。
(問1)アに当てはまる数を答えなさい。
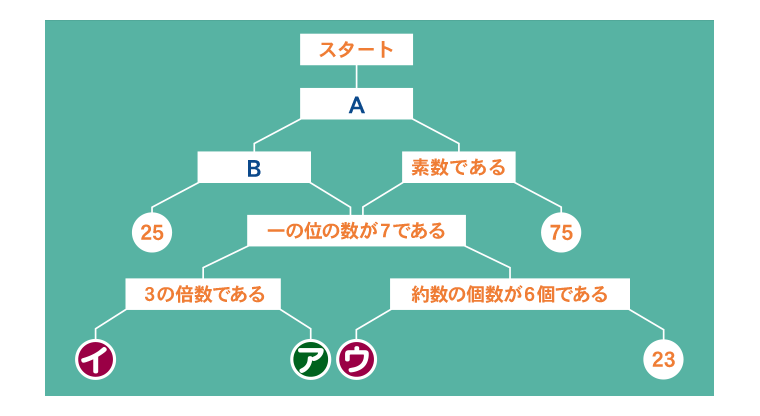
(問2)条件A、Bに当てはまる最も適切な条件を次の①〜⑤から選び、記号で答えなさい。
- ① 奇数である
- ② 50以下の数である
- ③ 約数の個数は奇数である
- ④ 各位の数の和が奇数である
- ⑤ 1種類の数を何回かかけ合わせてできる数である
(問3)イ、ウに当てはまる数を答えなさい。
中学入試問題は、子どもたちの“未来へ学び進むチカラ”を試しています。
そこには各中学の「こんなチカラを持った子どもを育てたい」というメッセージが込められています。
では、この学習院中等科の算数の入試問題には、どういうメッセージが込められていたのか、解答・解説と、日能研がこの問題を選んだ理由を見てみましょう。(出題意図とインタビューの公開日については更新情報をご確認ください。)
解答と解説
日能研による解答と解説
解答
(1)37
(2)A ⑤ B ③
(3)イ 27 ウ 32
解説
2、3、5、7から異なる2つの数を取り出して作ることができる2桁の数は、23、25、27、32、35、37、52、53、57、72、73、75の12種類です。この中の6種類の数が、図の「スタート」から振り分けられていきます。
(1)
まず、次の図1の太線のように振り分けられる数を考えます。アに当てはまる数は、「一の位の数が7であり」かつ「3の倍数ではない」数です。12種類の数の中で「一の位の数が7である」数は27、37、57です。これらの中で「3の倍数ではない」ものは37しかありません。よって、アに当てはまる数は37の1つに決まります。
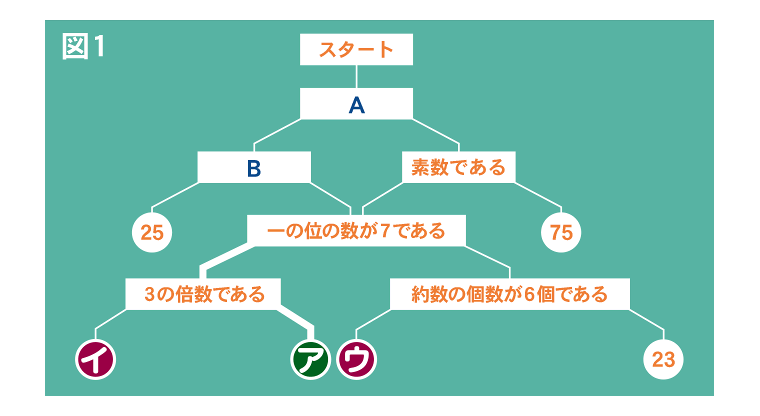
(2)
一番下の4つの数「イ、37(ア)、ウ、23」が図2の太線を通ったかどうかを調べます。
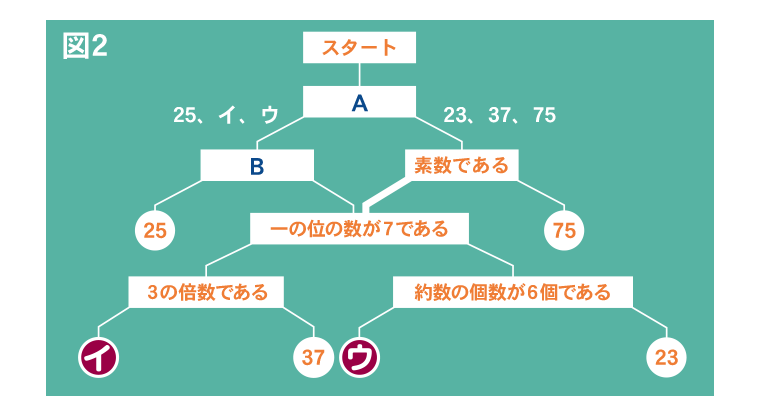
イに当てはまる数は「3の倍数」なので、太線を通っていません。また、ウに当てはまる数は「約数の個数が6個ある」ので素数ではありません。つまり、太線を通っていません。よって、Aから左へ振り分けられた3つの数は25、イ、ウと決まるので、図2の太線を通ってきたのは23と37とわかります。
したがって、条件Aに合う数の1つが25で、条件Aに合わない数が23、37、75です。①~⑤のうち、これらの4つの数をこのように振り分ける条件Aとして考えられるのは、③の「約数の個数は奇数である」と⑤の「1種類の数を何回かかけ合わせてできる数である」です。
③の条件に合う数は平方数の25(=5×5)だけです。
⑤の条件に合う数は25(=5×5)、27(=3×3×3)、32(=2×2×2×2×2)です。よって、条件Aを⑤の「1種類の数を何回かかけ合わせてできる数である」、条件Bを③の「約数の個数は奇数である」とすればよいことがわかります。(図3参照)
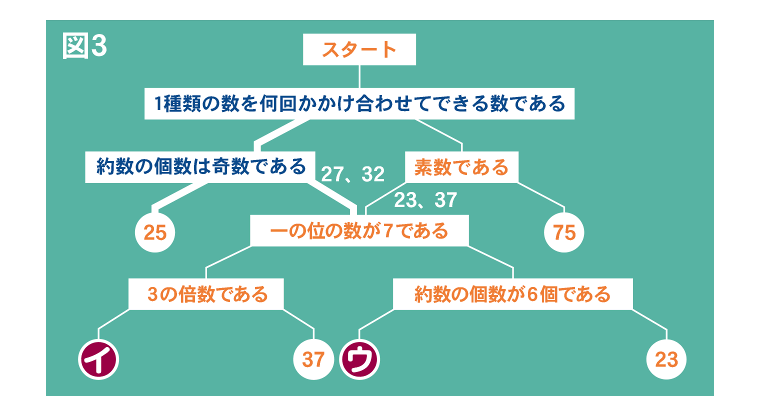
(3)
(2)より、イ、ウに当てはまる数は、27と32のどちらかです。イは一の位の数が7であるような数であることから27、ウは一の位の数が7ではなく、約数の個数が6個あるので32となります。
すべてを当てはめると、図4のようになります。
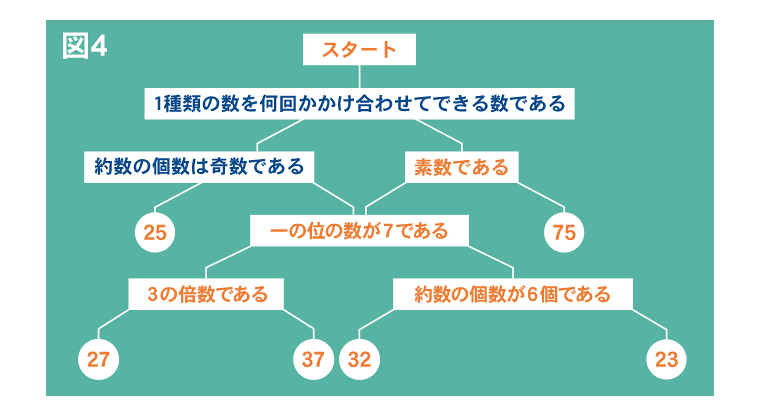
- 日能研がこの問題を選んだ理由
「数を分類し、振り分ける問題にもかかわらず、一番最初の条件と振り分ける数が提示されていない」というのがこの問題の最大の特徴です。示された条件をもとに、適切な数と条件を決定します。ただし、やみくもに、条件に合う数を手掛かりに、A、Bに当てはまる条件を決めようとしていたのでは、条件と数の両方を決定しなくてはならないために、かえって時間がかかってしまいます。この問題では、問題文の図の中にある一つひとつの条件や数の特徴を利用したり、組み合わせたり、時には利用しないことを選択したりしながら考え進める必要があります。複数の情報を整理し、情報の取捨選択をするチカラは、中学、高校、大学、そして社会に出た後にも、多くの場面で必要とされることでしょう。
このような理由から、日能研ではこの問題を□○シリーズに選ぶことに致しました。
