今月の額面広告に掲載されている問題はこれだ!
成城学園中学校
2014年08月掲載

2014年 成城学園中学校入試問題より
- 問題文のテキストを表示する
3辺のうち、2辺が10cm、15cmである三角形があります。このとき、残りの1辺の長さとして考えられる最も長い辺の長さは(ア)cmで、最も短い辺の長さは(イ)cmです。
ただし、(ア)、(イ)ともに整数とします。
中学入試問題は、子どもたちの“未来へ学び進むチカラ”を試しています。
そこには各中学の「こんなチカラを持った子どもを育てたい」というメッセージが込められています。
では、この成城学園中学校の算数の入試問題には、どういうメッセージが込められていたのか、解答・解説と、日能研がこの問題を選んだ理由を見てみましょう。(出題意図とインタビューの公開日については更新情報をご確認ください。)
解答と解説
日能研による解答と解説
解答
- (ア)24(cm)
- (イ)6(cm)
解説
三角形の3つの辺のうち、最も長い辺に着目します。
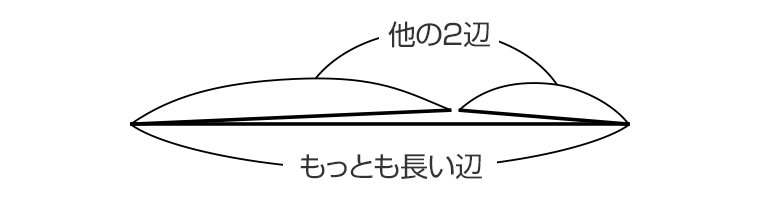
三角形には、「1つの辺の長さは他の2辺の長さの和よりも短い」という性質があります。なぜなら、最も長い辺の長さが他の2辺の長さの和と等しいか、それよりも長い場合、下の図のように、2辺が最も長い辺と重なってしまうため三角形にならないからです。
条件より、最も長い辺の長さは整数であることから、その長さは2辺の長さの和よりも1cm短いことがわかります。よって、残りの1辺が最も長い辺の場合、考えられる最も長い辺の長さは、(10+15)-1=24(cm)となります。
さらに、もし、最も長い辺の長さが15cmであるとしたら、他の2辺の長さの和は15cmより長くなければなりません。同じく、最も短い辺の長さも整数であるため、2辺の長さの和は15cmよりも1cm長いことがわかります。よって、考えられる最も短い辺の長さは(15+1)-10=6(cm)となります。
- 日能研がこの問題を選んだ理由
三角形を作るとき、3辺の長さの関係に着目して、辺の長さを決める必要があるため、辺の長さを常に自由に決められるわけではありません。この問題では、示されている状況から、考えられる場合を1つに決めず、その範囲をさぐっていく設定になっています。このとき、条件を満たすかどうかに意識を向けながら、限られた情報から状況を自分自身で設定して、問題を解決していくことが求められています。このようなチカラは、これからの時代を生きていく子ども達にぜひ身に付けてほしいチカラであるといえるでしょう。
このような理由から、日能研ではこの問題を□○シリーズに選ぶことに致しました。
