今月の額面広告に掲載されている問題はこれだ!
頌栄女子学院中学校
2015年12月掲載

2015年 頌栄女子学院中学校入試問題より
- 問題文のテキストを表示する
条件を入力すると、1から100までの整数のうちで条件に当てはまらない整数の個数を答えてくれるマシーンがあります。例えば条件「10以上」と入力すると「9個」と答え、条件「10の倍数」と入力すると「90個」と答えます。次の問いに答えなさい。
(問1)条件「2の倍数か、3の倍数か、5の倍数」を入力するとマシーンは何個と答えるでしょうか。
(問2)条件「4で割り切れないか、または 」と入力したらマシーンは「8個」と答え、条件「4で割り切れずに、さらに 」と入力したらマシーンは「33個」と答えました。 には同じ文が入ります。 にあてはまる文を答えなさい。
中学入試問題は、子どもたちの“未来へ学び進むチカラ”を試しています。
そこには各中学の「こんなチカラを持った子どもを育てたい」というメッセージが込められています。
では、この頌栄女子学院中学校の算数の入試問題には、どういうメッセージが込められていたのか、解答・解説と、日能研がこの問題を選んだ理由を見てみましょう。(出題意図とインタビューの公開日については更新情報をご確認ください。)
解答と解説
日能研による解答と解説
解答
(問1)26個
(問2)6で割り切れない
解説
(問1)
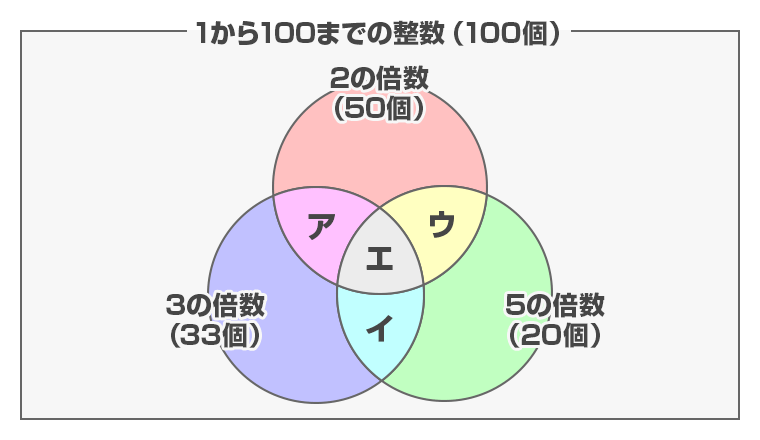
2の倍数は100÷2=50(個)あります。
3の倍数は100÷3=33余り1より、33個あります。
5の倍数は100÷5=20(個)あります。
2と3の公倍数は6の倍数なので、100÷6=16余り4より、16個あります。(図のア+エ)
3と5の公倍数は15の倍数なので、100÷15=6余り10より、6個あります。(図のイ+エ)
2と5の公倍数は10の倍数なので、100÷10=10(個)あります。(図のウ+エ)
2と3と5の公倍数は30の倍数なので、100÷30=3余り10より、3個あります。(図のエ)
よって、1から100までの整数の中で「2の倍数か、3の倍数か、5の倍数」は50+33+20-(16+10+6)+3=74(個)あることがわかります。
1から100までの整数の個数は100個あるので、マシーンは100-74=26(個)と答えます。
(問2)
にあてはまる文を明らかにするために、 にあてはまるものは何個あるのかを考えます。このとき、1から100までという範囲があることを利用して、あてはまるものとあてはまらないものの両方の個数に着目し、ベン図を用いて情報を増やしていきます。
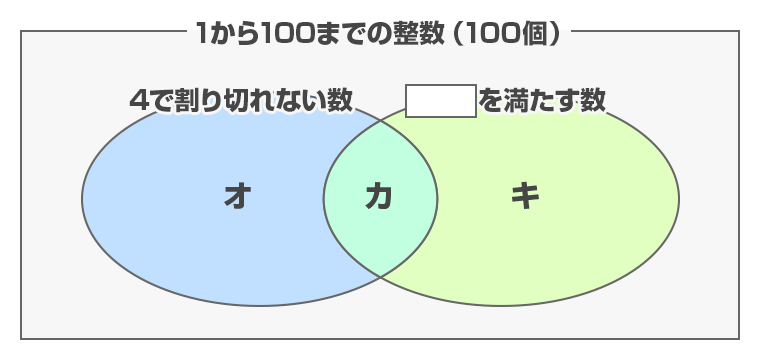
4で割り切れる数(4の倍数)は100÷4=25(個)あるので、4で割り切れない数は100-25=75(個)あります。(上の図のオ+カ)
条件「4で割り切れないか、または 」にあてはまる数は100-8=92(個)あります。(上の図のオ+カ+キ)
条件「4で割り切れずに、さらに 」にあてはまる数は100-33=67(個)あります。(上の図のカ)
よって、条件「4の倍数(4で割り切れる条件にあてはまらない数)で、さらに 」にあてはまる数は92-75=17(個)あることがわかります。(上の図のキ)
したがって、 の条件にあてはまる数は67+17=84(個)あることがわかります。(上の図のカ+キ)
以上、わかったことをベン図に整理すると、次のようになります。
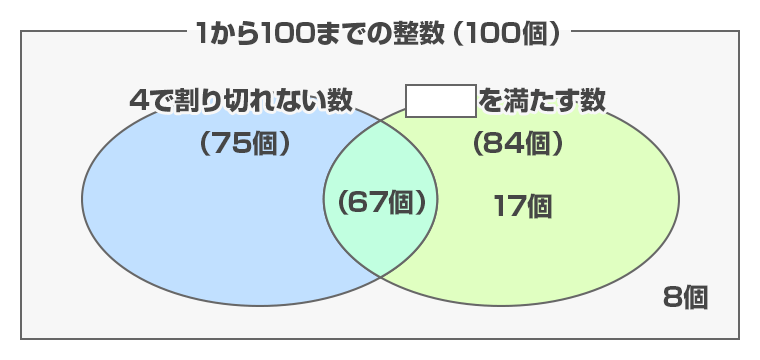
「 の条件にあてはまらない数」を「○で割り切れる数」とすると、「○で割り切れる数」つまり、○の倍数は100-84=16(個)あります。
100÷16=6余り4より、○=6とわかります。(4と6の公倍数は12の倍数なので、100÷12=8余り4より、8個あるので、条件を満たします。)
したがって、 には「6で割り切れない」があてはまります。
- 日能研がこの問題を選んだ理由
「条件に当てはまらない整数」とあるので、条件にあてはまらない整数を調べようと考えた人もいるかもしれません。しかし、1から100という範囲があるので、「条件に当てはまる整数」の個数を明らかにすれば、「条件に当てはまらない整数」の個数も明らかになります。
この問題では、問題文で示された言葉を言い換えたり、条件を図に置き換えたりしながら、状況を明らかにしていく力が求められています。既知の情報が持つ多面性を利用して、意図的にものの見方を変えることは、自分で状況を整理し、新たな情報を作り出していくことにつながります。このような力は、算数の問題に取り組むときに限らず、様々な未知の課題と出会ったときに必要とされるでしょう。
このような理由から、日能研ではこの問題を□○シリーズに選ぶことに致しました。
