今月の額面広告に掲載されている問題はこれだ!
鷗友学園女子中学校
2015年02月掲載

2014年 鷗友学園女子中学校入試問題より
※問1の解答欄は、最も多い本数の月日と最も少ない本数の月日の、両方を記入するようになっています。
- 問題文のテキストを表示する
棒を用いて、次のように数字を表します。
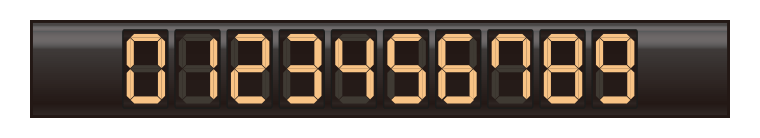
例えば、4月8日を表したいときは次のように2けたで表し、棒は23本必要です。
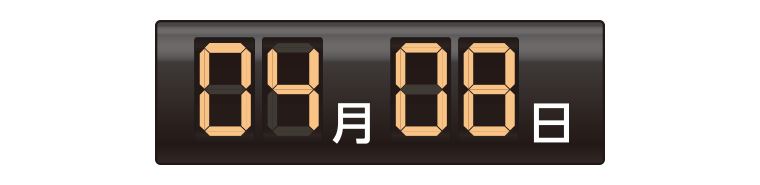
このとき、次の問いに答えなさい。
(問1)上のように月日を棒で表したとき、1年を通して最も多い本数と最も少ない本数の月日をそれぞれ答えなさい。
(問2)全部で24本の棒が必要な月日は何日ありますか。日数を答えなさい。
中学入試問題は、子どもたちの“未来へ学び進むチカラ”を試しています。
そこには各中学の「こんなチカラを持った子どもを育てたい」というメッセージが込められています。
では、この鷗友学園女子中学校の算数の入試問題には、どういうメッセージが込められていたのか、解答・解説と、日能研がこの問題を選んだ理由を見てみましょう。(出題意図とインタビューの公開日については更新情報をご確認ください。)
解答と解説
日能研による解答と解説
解答
(問1)最も多い日 8月8日、最も少ない日 11月11日
(問2)16日
解説
それぞれの数字で使われている棒の本数をまとめると、下のようになります。
| 数字 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|---|
| 本数 | 6 | 2 | 5 | 5 | 4 | 5 | 6 | 4 | 7 | 6 |
この表を利用しながら調べるとよいでしょう。
(問1)
「月の数」は01~12、「日の数」は01~31を調べます。
「月の数」、「日の数」ともに最大は「08」の6+7=13(本)、最小は「11」の2+2=4(本)です。
ですから、最も多い日は8月8日、最も少ない日は11月11日です。
(問2)
月日は4つの数字で表されます。ですから、棒の本数は最大でも「88月88日」の7×4=28(本)です。
求める月日の棒の本数は24本なので、この最大の場合から28-24=4(本)減らせばよいとわかります。
4本減らしたときの、4つの数字で使われる棒の本数の組み合わせは次の(1)~(5)の5通り考えられます。
(1)(7本、7本、7本、3本)
(2)(7本、7本、6本、4本)
(3)(7本、7本、5本、5本)
(4)(7本、6本、6本、5本)
(5)(6本、6本、6本、6本)
(1)~(5)で考えられる日付は、それぞれ次の通りです。
(1)(7本、7本、7本、3本)…なし(3本で表せる数字はない)
(2)(7本、7本、6本、4本)…「8、8、0か6か9、4か7」→なし
(3)(7本、7本、5本、5本)…「8、8、2か3か5、2か3か5」→なし
(4)(7本、6本、6本、5本)…「8、0か6か9、0か6か9、2か3か5」
→02月08日、03月08日、05月08日、06月28日、08月02日、08月03日、08月05日、08月20日、08月26日、08月29日、08月30日、09月28日
(5)(6本、6本、6本、6本)…「0か6か9、0か6か9、0か6か9、0か6か9」
→06月06日、06月09日、09月06日、09月09日
以上のように、全部で16日あります。
(参考)01~31のそれぞれの棒の本数は以下の通りです。この表を作って調べることもできます。
| 数字 | 01 | 02 | 03 | 04 | 05 | 06 | 07 | 08 | 09 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 本数(本) | 8 | 11 | 11 | 10 | 11 | 12 | 10 | 13 | 12 | 8 |
| 数字 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 本数(本) | 4 | 7 | 7 | 6 | 7 | 8 | 6 | 9 | 8 | 11 |
| 数字 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
| 本数(本) | 7 | 10 | 10 | 9 | 10 | 11 | 9 | 12 | 11 | 11 |
| 数字 | 31 | |||||||||
| 本数(本) | 7 |
- 日能研がこの問題を選んだ理由
この問題では、デジタル数字で使われる棒の本数で数の大小をとらえます。ですから、例えば「0」は、1けたの整数の中では大きい方の数で、1けたの整数の中では「8」が一番大きいという、何とも奇妙な世界に入ったような気持ちになります。それだけにこの問題は、慣れ親しんでいる数の大小の感覚を一旦捨て、新たな大小の感覚を持って考えなければならないという、とても新鮮な条件が設定されているところに面白さを感じました。また、この問題は、専門的な算数・数学の知識が不要です。一方で、正解にたどりつくためには、自分でもれなく調べあげるためのルールを決めて調べる必要があります。課題解決のために、その場で自らきまりを作って実行する力が求められているところに、これから学び進む子ども達が目指す姿を見ることができます。
このような理由から、日能研ではこの問題を□○シリーズに選ぶことに致しました。
