今月の額面広告に掲載されている問題はこれだ!
鎌倉女学院中学校
2014年04月掲載

2014年 鎌倉女学院中学校入試問題より
- 問題文のテキストを表示する
(問)図は、縦3cm、横15cmの長方形の紙3枚を重ねたものです。
水色の部分の面積が102cm2のとき、太線の長さの合計は cmです。
中学入試問題は、子どもたちの“未来へ学び進むチカラ”を試しています。
そこには各中学の「こんなチカラを持った子どもを育てたい」というメッセージが込められています。
では、この鎌倉女学院中学校の算数の入試問題には、どういうメッセージが込められていたのか、解答・解説と、日能研がこの問題を選んだ理由を見てみましょう。(出題意図とインタビューの公開日については更新情報をご確認ください。)
解答と解説
日能研による解答と解説
解答
64cm
解説
3枚の長方形の周りの長さの合計から、重なっている部分の長さの合計を引いて、太線の長さの合計を求めます。
3×15×3=135(cm2)……長方形の紙3枚の面積の合計
135-102=33(cm2)……重なった部分の面積の合計
長方形の紙を重ねたので、図1のように重なっている部分は高さ3cmの平行四辺形となっています。3つの平行四辺形の底辺をそれぞれ□cm、△cm、☆cmとして、底辺の長さの合計を求めます。
□×3+△×3+☆×3=33……重なった部分の面積の合計
(□+△+☆)×3=33
□+△+☆=11(cm)
また、図2のように3つの平行四辺形の底辺をそれぞれ■cm、▲cm、★cmとします。
■×3+▲×3+★×3=33……重なった部分の面積の合計
(■+▲+★)×3=33
■+▲+★=11(cm)
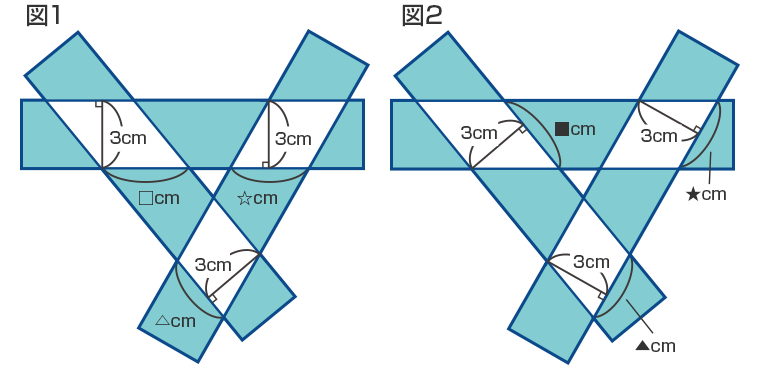
3つの平行四辺形の周りの長さの合計は、(□+△+☆)×2+(■+▲+★)×2と表すことができます。□+△+☆=11(cm)、■+▲+★=11(cm)より、3つの平行四辺形の周りの長さの合計は、11×2+11×2=44(cm)となります。
(3+15)×2×3=108(cm)……長方形の紙3枚の周りの長さの合計
108-44=64(cm)
- 日能研がこの問題を選んだ理由
重なっている部分を平行四辺形ととらえ、その周りの長さの合計に着目することで、一つひとつの辺の長さを求めることなく、平行四辺形の周りの長さの合計を知ることができます。そのとき、平行四辺形の底辺をどの辺としてとらえても高さが一定である点に目を向けることで、底辺の長さの合計を知るための指針を立てることができます。
部分一つひとつの総和である全体に着目できるチカラ、また、視点を変えても変化しない部分を利用できることに気づけるチカラは、これからの時代を生きていく子どもたちにぜひ身に付けてほしいチカラであるといえるでしょう。
このような理由から、日能研ではこの問題を□○シリーズに選ぶことに致しました。
