今月の額面広告に掲載されている問題はこれだ!
城北中学校
2016年04月掲載

2016年 城北中学校入試問題より
- 問題文のテキストを表示する
下図のように1cmごとに点が25個あります。4つの点を選んで、それらを頂点とする正方形を作ります。正方形1個の面積とその個数の関係を表にまとめました。
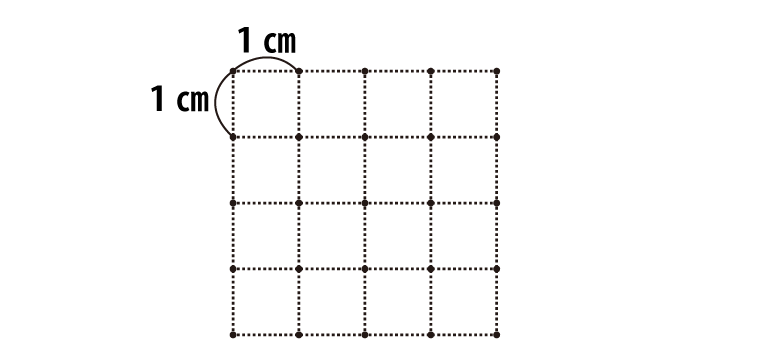
(問)下の表の にあてはまる数を求めなさい。
| 正方形1個の面積(cm2) | 1 | 2 | 4 | 5 | 9 | 16 | ||
|---|---|---|---|---|---|---|---|---|
| 個数 | 16 | 1 | 4 | 1 |
中学入試問題は、子どもたちの“未来へ学び進むチカラ”を試しています。
そこには各中学の「こんなチカラを持った子どもを育てたい」というメッセージが込められています。
では、この城北中学校の算数の入試問題には、どういうメッセージが込められていたのか、解答・解説と、日能研がこの問題を選んだ理由を見てみましょう。(出題意図とインタビューの公開日については更新情報をご確認ください。)
解答と解説
日能研による解答と解説
解答
| 正方形1個の面積(cm2) | 1 | 2 | 4 | 5 | 8 | 9 | 10 | 16 |
|---|---|---|---|---|---|---|---|---|
| 個数 | 16 | 9 | 9 | 8 | 1 | 4 | 2 | 1 |
解説
まず、まっすぐの向きの正方形について調べます。すると、1=1×1、4=2×2、9=3×3、16=4×4より、1cm2、4cm2、9cm2、16cm2の正方形は、次の(ア)~(エ)のようになることがわかります。
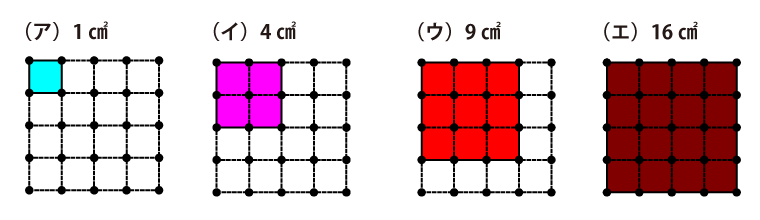
それぞれの個数を調べると、(ア)は16個、(イ)は9個、(ウ)は4個、(エ)は1個作ることができます。
ここまでにわかったことを表に書き込むと、次のようになります。
| 正方形1個の面積(cm2) | 1 | 2 | 4 | 5 | 9 | 16 | ||
|---|---|---|---|---|---|---|---|---|
| 個数 | 16 | 9 | 1 | 4 | 1 |
次に、斜めに辺をとる正方形を探すと、次の(オ)~(ク)の4種類が見つかります。
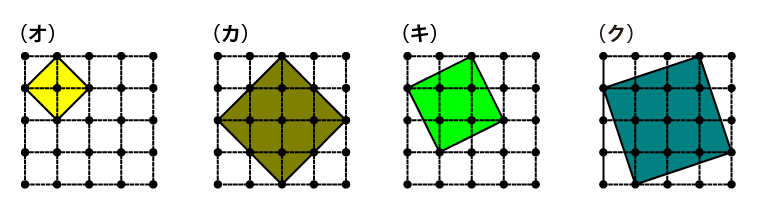
- (オ)2本の対角線の長さがいずれも2cmの正方形です。ですから、面積は2×2÷2=2(cm2)です。
この正方形は9個作ることができます。 - (カ)2本の対角線の長さがいずれも4cmの正方形です。ですから、面積は4×4÷2=8(cm2)です。この正方形は1個作ることができます。
-
(キ)1辺の長さが3cmの正方形から、下の図のように直角三角形を4個取りのぞいた形です。
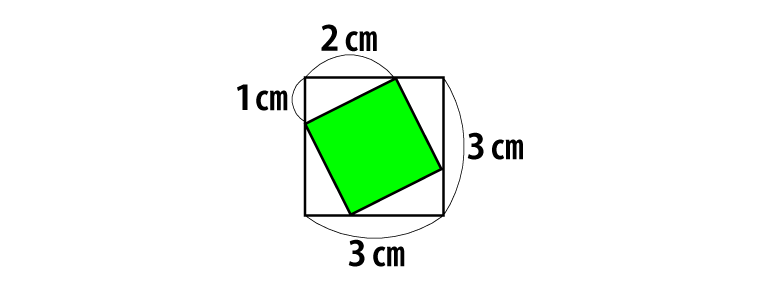
ですから、面積は3×3-1×2÷2×4=5(cm2)です。この正方形は、向きのちがいに注意すると、次のように8個作ることができます。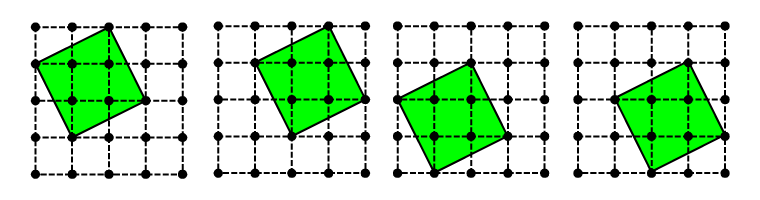
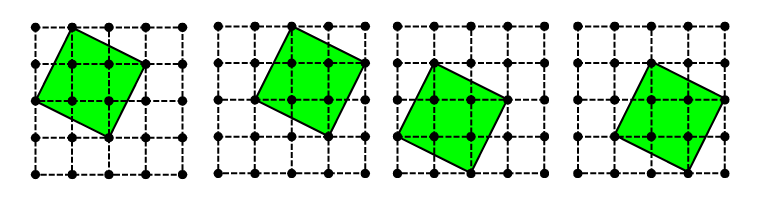
-
(ク)1辺の長さが4cmの正方形から、下の図のように直角三角形を4個取りのぞいた形です。
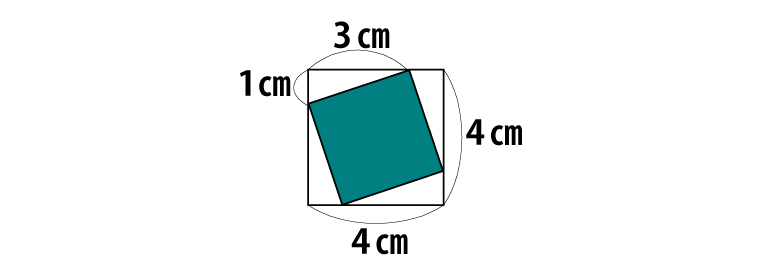
ですから、面積は4×4-1×3÷2×4=10(cm2)です。この正方形は、向きのちがいに注意すると、次のように2個作ることができます。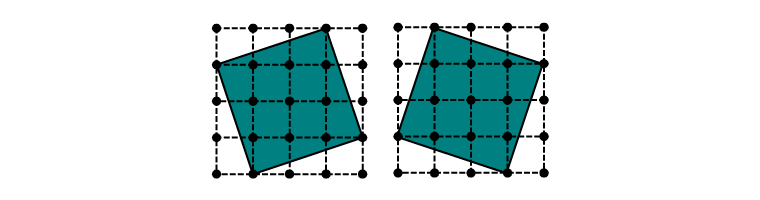
以上のことも表に書き込むと、次のようになります。
| 正方形1個の面積(cm2) | 1 | 2 | 4 | 5 | 8 | 9 | 10 | 16 |
|---|---|---|---|---|---|---|---|---|
| 個数 | 16 | 9 | 9 | 8 | 1 | 4 | 2 | 1 |
- 日能研がこの問題を選んだ理由
今回の問題で扱っている題材。中学受験に向けて学んできた子ども達は何度か目にしたことがあるものでしょう。このような問題では、多くの場面で、次のように問われます。
「25個の点のうち、4つの点を頂点とする正方形を作ります。このとき、正方形を全部で何個作ることができますか。」
今回の問題の最大の特徴は、表が最初から提示されていることです。そして、表の中には作ることができる正方形が8種類であることや、いくつかの正方形の面積や作ることができる個数など、考える手がかりがいくつか示されています。
では、手順が見えたことで問題の中の何かが損なわれたのかというと、取り組んでみるとそうではないことに気づきます。むしろ、単に「正方形を全部で何個作ることができますか」と問うのではなく、表に示された数値を用いることで、取り組む私たちに“調べ方”を伝えてくれていることを感じます。
問題に取り組みやすくするさまざまな工夫からは、少し高級な問題を多くの子どもに取り組んでほしい、味わってほしい、そして中学入試の場面であっても解きながら学んでほしいという学校の想いを感じました。
このような理由から、日能研ではこの問題を□○シリーズに選ぶことに致しました。
