今月の額面広告に掲載されている問題はこれだ!
神奈川大学附属中学校
2015年08月掲載

2015年 神奈川大学附属中学校入試問題より
- 問題文のテキストを表示する
1から50までの番号が1つずつ書かれた50個のボールがあります。Pさんが、1番のボールから50番のボールまで、番号順にレールの上を転がします。Aさん、Bさん、Cさんの3人は、そのレールのそばに一列に並び、次のルールに従ってボールを取っていきます。
【ルール】
- Aさんは、2の倍数の番号のボールが目の前に転がってきたら必ず取る。
- Bさんは、3の倍数の番号のボールが目の前に転がってきたら必ず取る。
- Cさんは、5の倍数の番号のボールが目の前に転がってきたら必ず取る。
- 3人がいずれも取らなかったボールは、箱の中に入る。
- 3人のいずれかがボールを取るか、またはボールが箱の中に入ったら、Pさんは次の番号の書かれたボールを転がす。
(問)
Bさんは24番のボールを、Cさんは45番のボールを取ることができるとき、Aさん、Bさん、Cさんの3人はPさんに近い方からどのような順で並んでいますか。
また、このときAさんは全部で何個のボールを取ることができますか。
中学入試問題は、子どもたちの“未来へ学び進むチカラ”を試しています。
そこには各中学の「こんなチカラを持った子どもを育てたい」というメッセージが込められています。
では、この神奈川大学附属中学校の算数の入試問題には、どういうメッセージが込められていたのか、解答・解説と、日能研がこの問題を選んだ理由を見てみましょう。(出題意図とインタビューの公開日については更新情報をご確認ください。)
解答と解説
日能研による解答と解説
解答
[並び順] Cさん、Bさん、Aさんの順
[Aさんが取った個数] 13個
解説
24=2×2×2×3より、24は2の倍数でも3の倍数でもあります。つまり、24番のボールは、AさんとBさんのうち、Pさんに近いところに並んでいる人が取ることになります。問題文に「Bさんが24番を取ることができる」とあることから、AさんよりもBさんの方がPさんに近いところに並んでいることがわかります。
45=3×3×5より、45は3の倍数でも5の倍数でもあります。つまり、45番のボールは、BさんとCさんのうち、Pさんに近いところに並んでいる人が取ることになります。問題文に「Cさんが45番のボールを取ることができる」とあることから、BさんよりもCさんの方がPさんに近いところに並んでいることがわかります。
以上のことを合わせると、Pさんに近い方から「Cさん、Bさん、Aさん」の順に並んでいることがわかります。
AさんはPさんから一番離れたところに並んでいるため、Aさんが取ることができるボールに書かれた数(番号)は、2の倍数のうち、3の倍数と5の倍数を除いたものです。
2の倍数、3の倍数、5の倍数の関係を下のような図に表すと、アの部分に入る数の個数を求めればよいことがわかります。
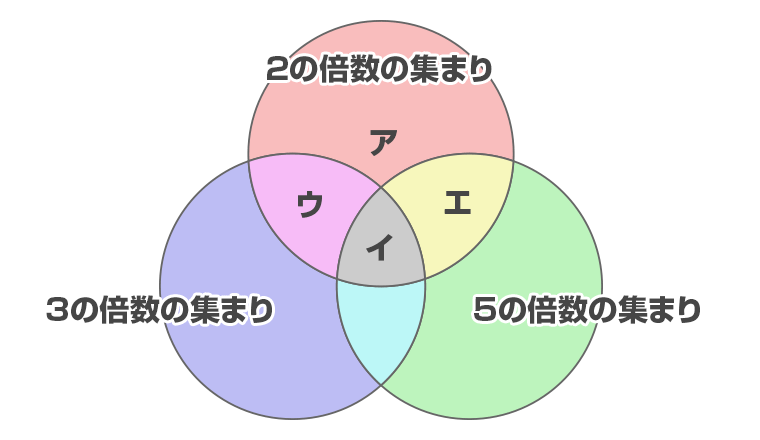
50÷2=25より、ア+イ+ウ+エは25個です。
2と3と5の最小公倍数は30なので、50÷30=1余り20より、イは1個です。
2と3の最小公倍数は6なので、50÷6=8余り2より、イ+ウは8個です。つまり、ウは8-1=7(個)です。
2と5の最小公倍数は10なので、50÷10=5より、イ+エは5個です。つまり、エは5-1=4(個)です。
以上より、アは25-(1+7+4)=13(個)となります。
- 日能研がこの問題を選んだ理由
この問題で与えられた情報は「全体のルール」と「Bさんが24番、Cさんが45番のボールを取った」ということだけです。たったこれだけの情報で、3人が並んでいる順番や、それぞれが取ったボールの個数を知ることができるのです。
与えられた情報の裏にはどのようなことが隠れているのかを探り、論理的な正しさを保ちつつ自分で新たな情報を作り出していく力は、これからの時代を生きていく子ども達にぜひ身に付けてほしい力であるといえるでしょう。このような理由から、日能研ではこの問題を□○シリーズに選ぶことに致しました。
