今月の額面広告に掲載されている問題はこれだ!
桐蔭学園中学校・中等教育学校
2015年06月掲載

2015年 桐蔭学園中学校・中等教育学校入試問題より
- 問題文のテキストを表示する
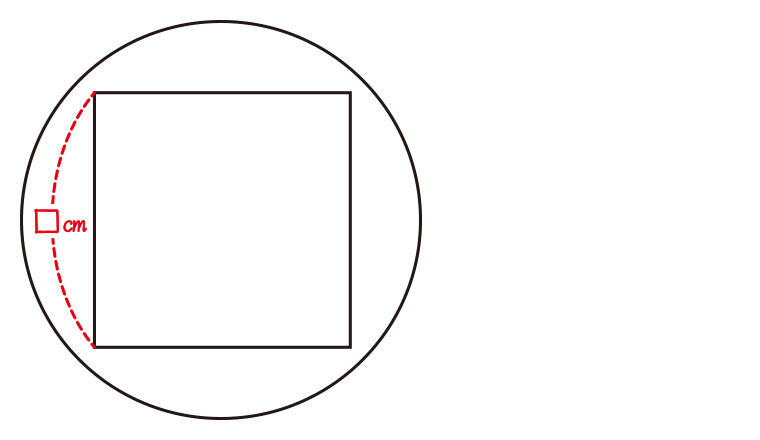
半径が10㎝の円の中に入る正方形の1辺の長さは□㎝です。□にあてはまる最も大きい整数はいくつですか。どのように考えて求めたのか、式や考え方も答えなさい。
中学入試問題は、子どもたちの“未来へ学び進むチカラ”を試しています。
そこには各中学の「こんなチカラを持った子どもを育てたい」というメッセージが込められています。
では、この桐蔭学園中学校・中等教育学校の算数の入試問題には、どういうメッセージが込められていたのか、解答・解説と、日能研がこの問題を選んだ理由を見てみましょう。(出題意図とインタビューの公開日については更新情報をご確認ください。)
解答と解説
日能研による解答と解説
解答
□の解答 14
半径10cmの円の中には、対角線の長さが20cmの正方形がぴったりと入る。その正方形の面積は20×20÷2=200(cm2)なので、これより小さい正方形を考える。14×14=196、15×15=225だから、□にあてはまる整数は14以下とわかり、最大は14となる。
解説
10×2=20(cm)……半径10cmの円に入る最大の正方形の対角線の長さ
20×20÷2=200(cm2)……半径10cm円に入る最大の正方形の面積
正方形の1辺の長さは整数になるので、200以下で200に最も近い平方数を考える。
14×14=196(cm2)……1辺14cmの正方形の面積
15×15=225(cm2)……1辺15cmの正方形の面積
よって、□にあてはまる数は14である。
- 日能研がこの問題を選んだ理由
桐蔭学園中学校・中等教育学校の大設問5(4)からの紹介です。
この問題はおそらく本来ならば平方根で考えたいが、整数という数値設定にして小学生でも考えられるようにしているところが興味深く感じられました。また、この問題では、円の面積を調べたり、円の直径と円の中に入る正方形との関係を考えたりする中で、面積の範囲をとらえ、条件に合う数値を調べていくことになります。この問題のように、図形の問題に見えながら、数を処理する力を問うている点がユニークであると感じました。今後の子どもたちが、未知の事柄と出あった際に「自ら課題を見つけ解決するチカラ」を養うためのよい助けになると思います。
このような理由から、日能研ではこの問題を□○シリーズに選ぶことに致しました。
