今月の額面広告に掲載されている問題はこれだ!
東洋英和女学院中学部
2014年10月掲載
2014年 東洋英和女学院中学部入試問題より
- 問題文のテキストを表示する
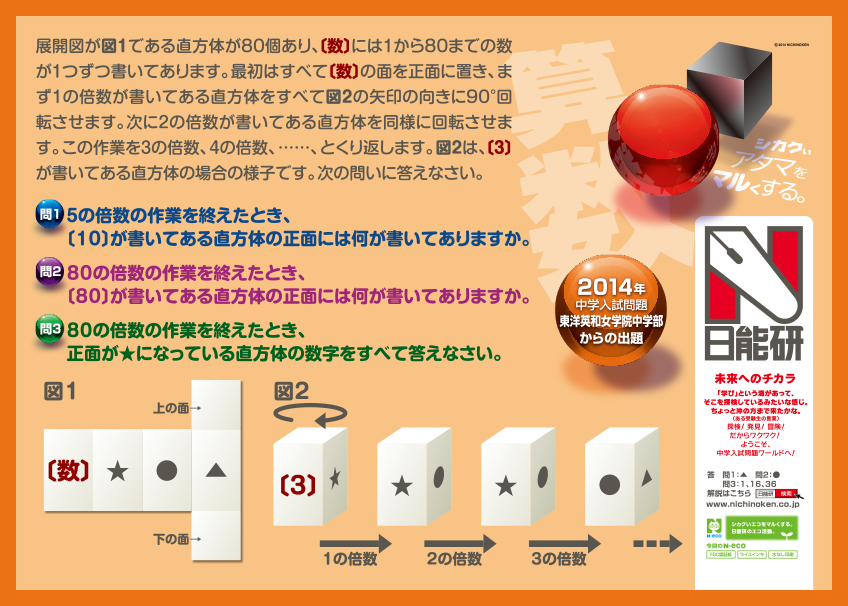
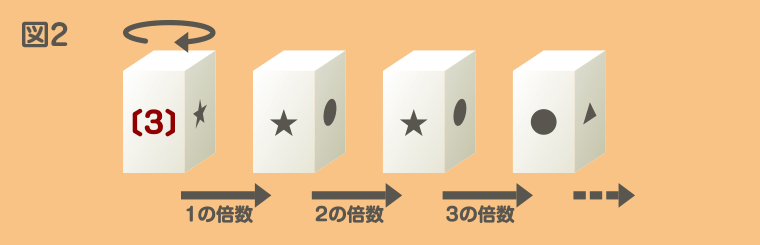
展開図が図1である直方体が80個あり、〔数〕には1から80までの数が1つずつ書いてあります。最初はすべて〔数〕の面を正面に置き、まず1の倍数が書いてある直方体をすべて図2の矢印の向きに90°回転させます。次に2の倍数が書いてある直方体を同様に回転させます。この作業を3の倍数、4の倍数、……、とくり返します。図2は、〔3〕が書いてある直方体の場合の様子です。次の問いに答えなさい。

(問1)5の倍数の作業を終えたとき、〔10〕が書いてある直方体の正面には何が書いてありますか。
(問2)80の倍数の作業を終えたとき、〔80〕が書いてある直方体の正面には何が書いてありますか。
(問3)80の倍数の作業を終えたとき、正面が★になっている直方体の数字をすべて答えなさい。
中学入試問題は、子どもたちの“未来へ学び進むチカラ”を試しています。
そこには各中学の「こんなチカラを持った子どもを育てたい」というメッセージが込められています。
では、この東洋英和女学院中学部の算数の入試問題には、どういうメッセージが込められていたのか、解答・解説と、日能研がこの問題を選んだ理由を見てみましょう。(出題意図とインタビューの公開日については更新情報をご確認ください。)
解答と解説
日能研による解答と解説
解答
- (問1)▲
- (問2)●
- (問3)1、16、36
解説
立体を90度回転させる度に、立体の正面は、「★、●、▲、〔数〕、★、●、▲、〔数〕、…」と規則正しく変化していくことと、〔数〕の約数の個数に着目します。「□の倍数が書いてある直方体を90度回転させる」の□には、回転させる直方体の〔数〕の約数が入ります。つまり、回転させる回数と約数の個数は一致します。
- (問1)〔10〕の約数は、1、2、5、10です。ですから、1の倍数、2の倍数、5の倍数のときに90度回転させることがわかります。つまり、5の倍数の作業を終えたとき、90度回転を3回させることになるので、直方体の正面には「▲」が書いてあります。
- (問2)〔80〕の約数は、1、2、4、5、8、10、16、20、40、80の10個です。つまり、80の倍数の作業を終えたとき、90度回転を10回させることになるので、10÷4=2余り2より、直方体の正面には「●」が書いてあります。
- (問3)「★」が正面になるためには、90度回転を1回、5回、9回、13回、17回、…させる必要があります。つまり、〔数〕の約数の個数が1個、5個、9個、13個、17個、…の場合であることがわかります。このとき、約数の個数は奇数個です。約数を奇数個持つ数は平方数です。1~80までのうち、平方数は1、4、9、16、25、36、49、64です。このうち、約数が1個の〔数〕は〔1〕、約数が5個の〔数〕は〔16〕、約数が9個の〔数〕は〔36〕なので、1、16、36とわかります。
- 日能研がこの問題を選んだ理由
立体を構成する面の位置の関係をとらえた上で、数を構成する要素に目を向けて、先の変化を予測していきます。具体的な場合を実際に調べていくことは現実的ではありません。そこで、「立体を4回転させると元の位置に戻る周期」と、「回転させる回数と約数の個数は一致するという事実」を複合して、必要な情報を獲得していきます。複数の情報に目を向け、使いやすい形に置き換えて、それら組み合わせて利用していく、このようなチカラは、これからの時代を生きていく子ども達にぜひ身に付けてほしいチカラであるといえるでしょう。
このような理由から、日能研ではこの問題を□○シリーズに選ぶことに致しました。
